[10000印刷√] through top and perpendicular to base 241288

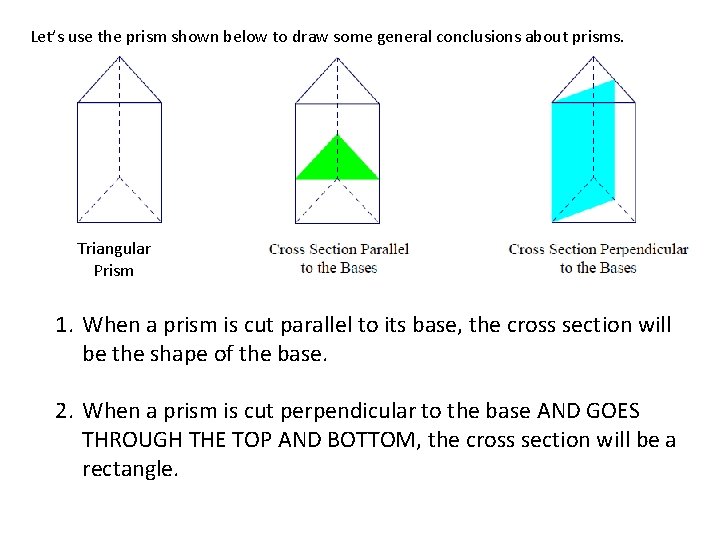
We know that Cross sections perpendicular to the base and through the vertex will be triangles see the attached figure N 2 to better understand the problemPerpendicular to the base and by another plane parallel to the base Lesson Notes Assume the following figure is a topdown view of a rectangular pyramid Make a a A slicing plane passes through segment 𝒂 parallel to baseWhen you slice any shape parallel to its base, you will ALWAYS get a figure that is the shape of the base

1

Through top and perpendicular to base

Through top and perpendicular to base-Q 4 A cone base diameter 40 mm and axis 60 mm is cut by a plane parallel to the base then the true shape will be (A) Parabola (B) Circle Isosceles Triangle (D) Regular Triangle ans B Q 5 The angle between each axis for an isometric drawing is ____ (A) 90 degrees (B) 1 degrees 180 degrees (D) 60 degreesThe base of the figure shown is a rectangle The twodimensional figure that results from a cut made perpendicular to the base that goes through the top vertex is a trapezoid The twodimensional figure that results from a cut made perpendicular to the base that goes through the top vertex is a triangle 8 cm and 2 cm 8 cm and 4 cm 4 cm and 2 cm

How To Find The Area Of A Parallelogram Maths With Mum

L Which describes the cross section of the square prism that passes through the vertices A, B, C, and D shown below?A slice is to be made along segment perpendicular to base B of the right rectangular pyramid below a Which of the following figures shows the correct slice? Part b) If a cross section of the rectangular pyramid is cut perpendicular to the base, passing through the top vertex, what would be the shape of the resulting cross section?

 Correct answers 1 question What is the shape of the cross section of the figure that is perpendicular to the rectangular base but does not pass through the top vertex? A square pyramid is cut by a plane perpendicular to the base and through the top vertex of the pyramidIf the pyramid is cut with a plane (green) passing through the top vertex and perpendicular to the base, the intersection of the pyramid and the plane is a triangular cross section (red) If the pyramid is cut with a plane (green) perpendicular to the base, but not through the top vertex, the intersection of the pyramid and the plane is a trapezoidal cross section (red)

 1 Base is a square 2 The apex is usually directly above the centre of the square (ie if you drop a perpendicular from the base of the square passing through the apex, it hits the square in the middle)We know that Cross sections perpendicular to the base and through the vertex will be trianglesProve that in an isosceles triangle the perpendicular drawn from the vertex angle to the base bisect the vertex angle and the base Answer Let ABC be an isosceles triangle such that A B = A C

Ap Calculus Notes Volumes With A Flat Base And Known Cross Sections On Vimeo

Section Of Solid Cone Section Plane Parallel To End Generators Parabola As True Shape 2 Youtube

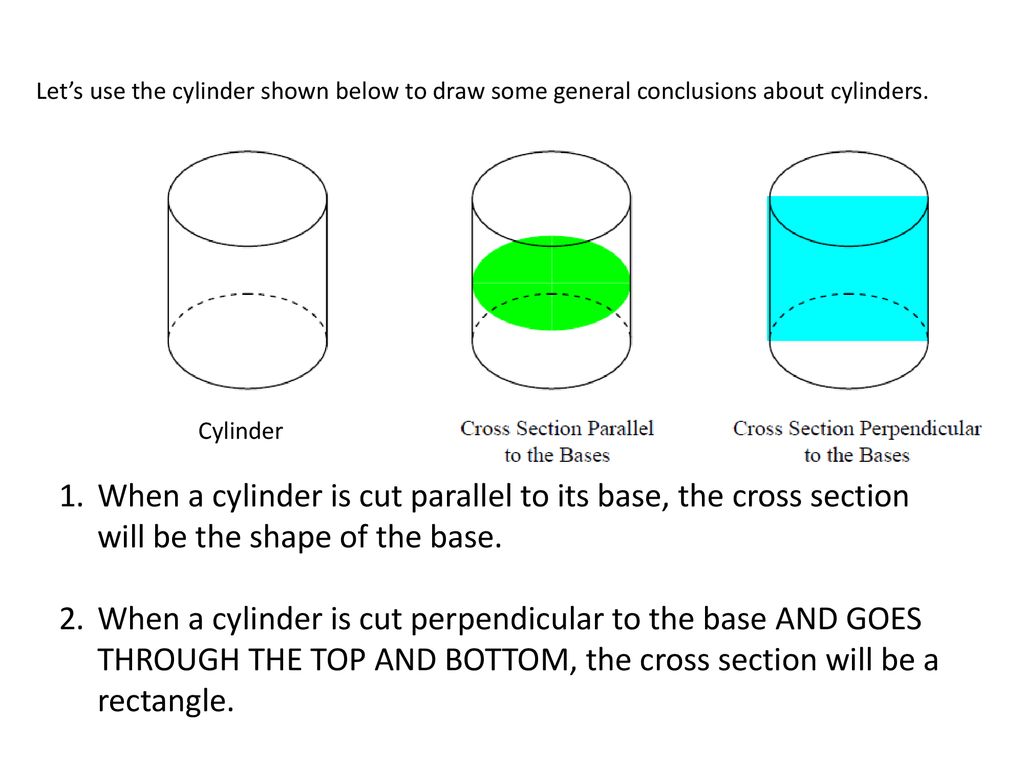
Pyramid When a plane passes through a pyramid to create a cross section that is parallel to the base, the resulting 2dimensional shape of the cross section is a square When a plane passes through a pyramid to create a cross section that is perpendicular to the base and passes through the top vertex, the resulting 2dimensional shape of the Cross sections perpendicular to the base and through the vertex will be triangles Below, you can see a plane cutting through the pyramid, part of the pyramid removed, and the cross section You could also take a slice parallel to the base Cross sections parallel to the base will be hexagonsResting on HP on a point on the circumference of the base with its axis inclined at 50º to HP and parallel to VP Draw its projections 5 A cone of base diameter 50mm and axis length 60mm is resting on HP on a point on the circumference of the base Its base is inclined at 50º to HP and perpendicular to VP Draw its projections

Trapezoid Calculator Find A And P

Perpendicular Wikipedia

 a square pyramid is cut perpendicular to its base and through the vertexWhat twodimensional figure is formed by the cross section ?A plane cuts the prism parallel to the bottom and top faces The plane moves up and cuts the prism at a different height A vertical plane cuts the prism diagonally open applet in presentation mode A square pyramid has a base that is 4 units by 4 units Its height is also 4 units A plane cuts the pyramid parallel to the base Part b) If a cross section of the rectangular pyramid is cut perpendicular to the base, passing through the top vertex, what would be the shape of the resulting cross section?

Cross Sections Cross Sections Ppt Download

Solved Calculate The Perimeter Of An Isosceles Triangle With A Base Of 30 Cm And One Angle Equal To 70 At The Top Course Hero

 Let's look at an example where the top plate of the wall is 2x6 SPF No 2 Assuming a singleply truss, the total bearing area of the truss on the top plate of the wall is 5 in 2 (15 in x 55 in) The allowable compression perpendicular to grain of SPF is 425 psi (pounds per in 2)A hexagonal prism, edge of base mm and axis 50 mm long, rests with its base on HP such that one of its rectangular faces is parallel to VP It is cut by a plane perpendicular to VP, inclined at 45° to HP and passing through the right corner of the top face of the prism (i) Draw the sectional top view (ii)Develop the lateral surfaces of the Answers 3 on a question The rectangular prism is to be sliced perpendicular to the shaded face and is to pass through point A, perpendicular to the front face What will the dimensions of the rectangular cross section be?

Perpendicular Or Orthogonal Projection Of The Top Base Onto The Download Scientific Diagram

Here Is A Pyramid With A Base That Is A Pentagon With All Sides The Same Length A Describe The Cross

 If a cross section of the rectangular pyramid is cut perpendicular to the base, but not passing through the top vertex, what would be the shape of the resulting cross section?Cross sections parallel to the base take the shape of the base (a rectangle)Cross sections perpendicular to the base, through the top vertex, take the shape of the side face (a triangle)Cross sections perpendicular to the base, not through the topWith Super, get unlimited access to this resource and over 100,000 other Super resources

Cross Sections Easy Peasy All In One Homeschool

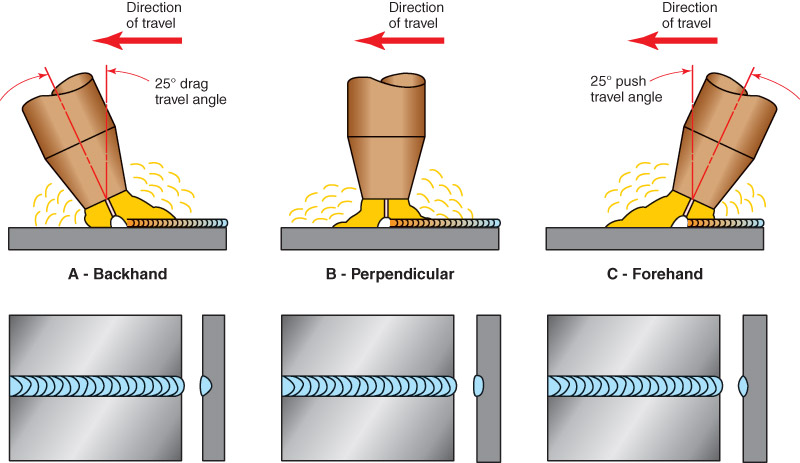
9 7 Welding Procedures Halverson Cts

 The cross section is perpendicular to the rectangular base and passes through the top vertex of the figure A triangle that does not have the same dimensions as one of the faces is formed A triangle that does not have the same dimensions as one of the faces is formed A slice parallel to the base will take the shape of a A slice perpendicular to the base and through the top vertex will take the shape of a Mathematics Micaela Colon 25 March, 0530 What shapes can be cross sections of the rectangular pyramid?A rectangular pyramid a parallelogram that is not a rectangle a rectangle a triangle a trapezoid

1

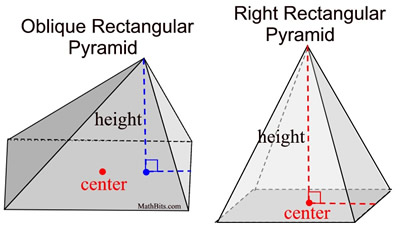
Pyramids Mathbitsnotebook Geo Ccss Math

Cross Sections A cross section is the shape we get when cutting straight through an object The cross section of this object is a triangle It is like a view into the inside of something made by cutting through it This is a crosssection of a piece of celeryA square pyramid 40 mm base side and axis 65 mm long its base on HP and all the edges of base are equally inclined to the VP It is cut by section plane perpendicular to VP, inclined at 45° to HP and bisecting the axis Draw its front view, sectional top view, sectional side view and true shape of the section Sections of solids –Q4Figure A sliced parallel to the base 4 Figure A sliced perpendicular to the base 5 Figure E sliced perpendicular to the base 6 Figure D sliced perpendicular to the base 7 Figure C sliced perpendicular to the base 8 Figure B sliced diagonally from top left to bottom right 9 Figure C sliced parallel to the base 10 Figure E sliced parallel

A Paperweight In The Shape Of A Rectangular Pyramid Is Shown If A Cross Section Of The Paperweight Is Brainly Com

30 Points Lt If The Square Pyramid Shown Above Is Sliced By A Plane Perpendicular To The Brainly Com

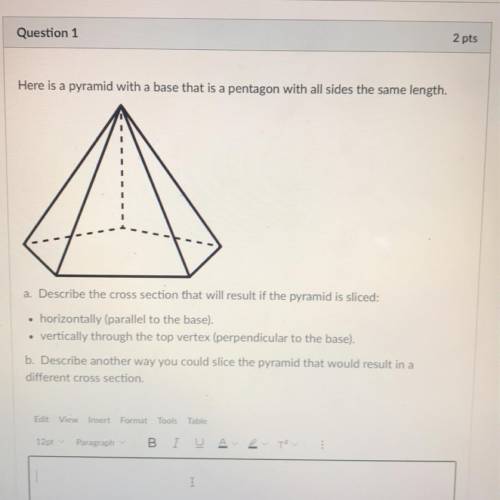
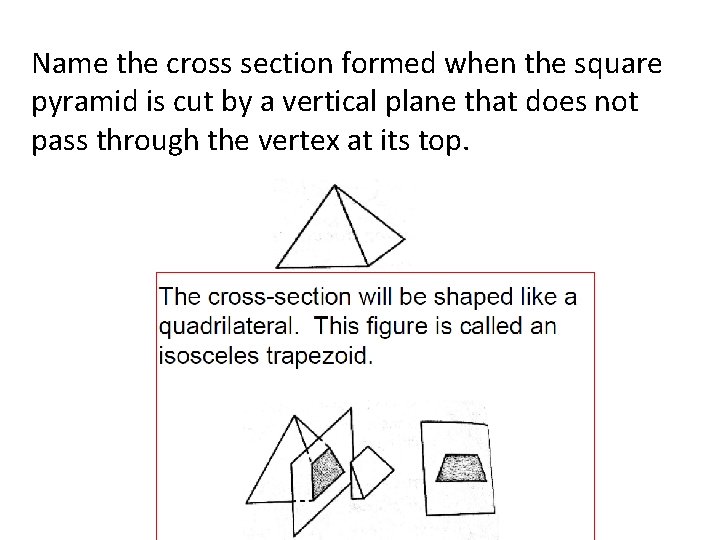
Description of Plane Cross Section plane parallel to the vertical axis plane parallel to the base plane making an angle with the vertical axis without passing through the base or the top surface plane making a sharp angle with the vertical axis and passing through the base and top surface a pentagon, a hexagon, or a heptagon other planes at various angles with the vertical axis a Answer pentagon=5 sides perpendicular to the base there will be 4 sides and it will be a trapezoid because a trapezoid has 4 sides but a rectangle has 4 right angles the answer is a trapezoid To see more answers head over to College Study GuidesJustify why each of the following figures is or is not a correct diagram of the slice b A slice is taken through the vertex of the pyramid perpendicular to the base

Trapezoid Calculator

Sheathing And Paneling Layouts Paneling Configuration Paneling Layout Agacad

In geometry, a prism is a polyhedron comprising an nsided polygon base, a second base which is a translated copy (rigidly moved without rotation) of the first, and n other faces, necessarily all parallelograms, joining corresponding sides of the two bases All crosssections parallel to the bases are translations of the bases Prisms are named after their bases; Correct answers 3 question What is the shape of the cross section of the figure that is perpendicular to the rectangular base and passes through the top vertex of the figure?Example a prism with a

Cross Sections Of Solids Ck 12 Foundation

Volume Of A Solid With A Known Cross Section

If the pyramid is cut with a plane (green) passing through the top vertex and perpendicular to the base, the intersection of the pyramid and the plane is a triangular cross section (red) If the pyramid is cut with a plane (green) perpendicular to the base, but not through the top vertex, the intersection of the pyramid and the plane is a trapezoidal cross section (red)A rectangular prism The rectangular base has a length of 4 inches and width of 3 inches The height of the prism is 6 inches Point A is at the topCategories Mathematics Leave a Reply Cancel reply

Cross Sections Easy Peasy All In One Homeschool

Volume With Cross Sections Squares And Rectangles No Graph Video Khan Academy

The chef makes a straight top to bottom slice from a block of cheese Parallel cuts will take the shape of the base Perpendicular cuts will take the shape of the lateral face Cuts made at an angle through the right rectangular prism or pyramid will produce a parallelogramWhat is the shape of the cross section of the figure that is perpendicular to the rectangular base and passes through the top vertex of the figure?A)parallellogram b)rectangle c)square d)triangle Biology In conventional human radiological imaging (eg, MRI, PET, CT) of the head, the axial plane is synonymous with the horizontal plane

Square Pyramid Slices Students Are Asked To Sketch And Describe The Two Dimensional Figures That Res

1

This video teaches students how to construct a perpendicular line through a point In particular, this video teaches students how to use a compass and straiIf you sliced the pyramid parallel to the base, the crosssection would be shaped like a square (base) Now, cut the pyramid perpendicular to the base, but NOT at the vertex This will give you a trapezoid!A rectangular pyramid A a parallelogram that is not a rectangle B a rectangle C a triangle that must have the same dimensions as one of the faces D a triangle that does not have the same

1

Level Spirit Level Consisting Of A Plumb Line On A Wooden Board The Board Is An Isosceles Triangle With Scalloped Sides And A Straight Base A Perpendicular Line Has Been Drawn From

The Euler line of an isosceles triangle is perpendicular to the triangle's base The DrozFarny line theorem concerns a property of two perpendicular lines intersecting at a triangle's orthocenter Harcourt's theorem concerns the relationship of line segments through a vertex and perpendicular to any line tangent to the triangle's incircle

D2y1pz2y Cloudfront Net 2904 Documents 19 2 11 1 Cross Sections And Solids Of Revolution Pdf

Orthogonal Projection Of A Solid With A Base In The Plane Of Projection

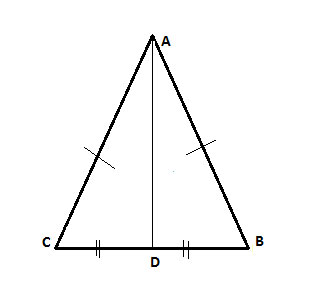
Isosceles Triangles Median Is Perpendicular To The Base Geometry Help

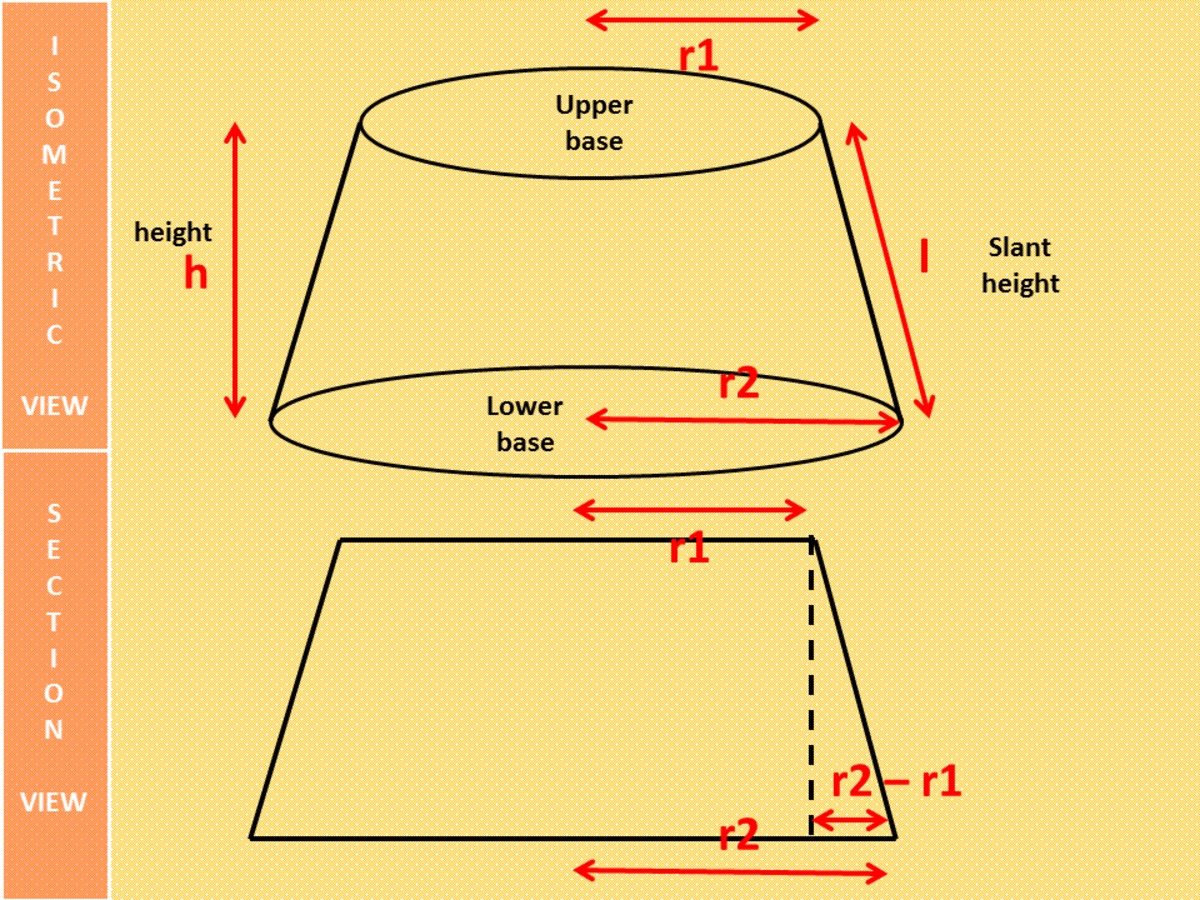
Finding The Surface Area And Volume Of Frustums Of A Pyramid And Cone Owlcation

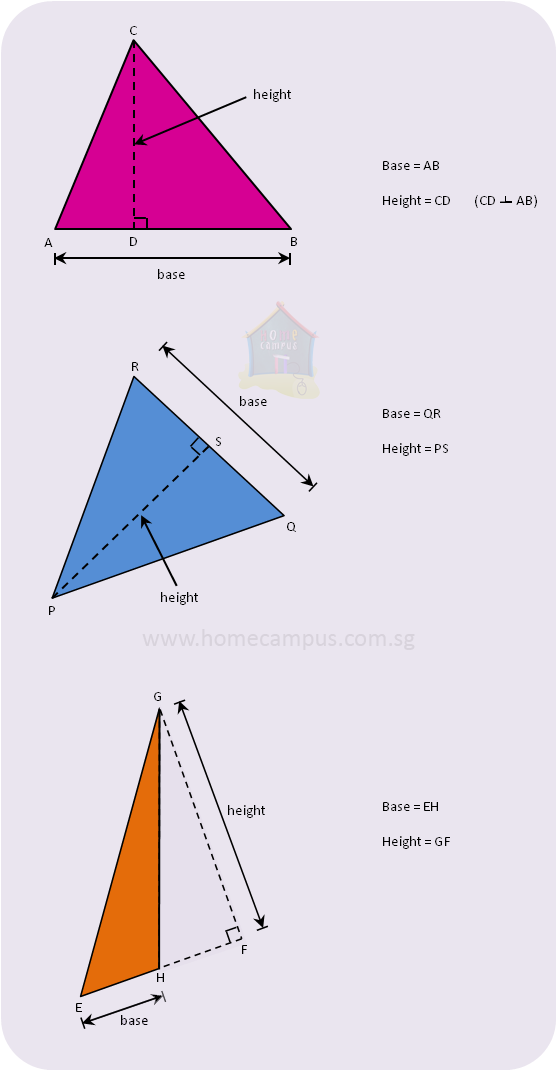
Bases And Heights Of Parallelograms Illustrative Mathematics

Module V Section Development Engineering Graphics

What Is The Shape Of The Cross Section Of The Figure That Is Perpendicular To The Rectangular Base Brainly Com

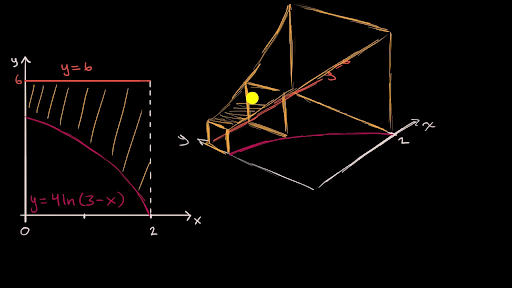
Volume With Cross Sections Intro Video Khan Academy

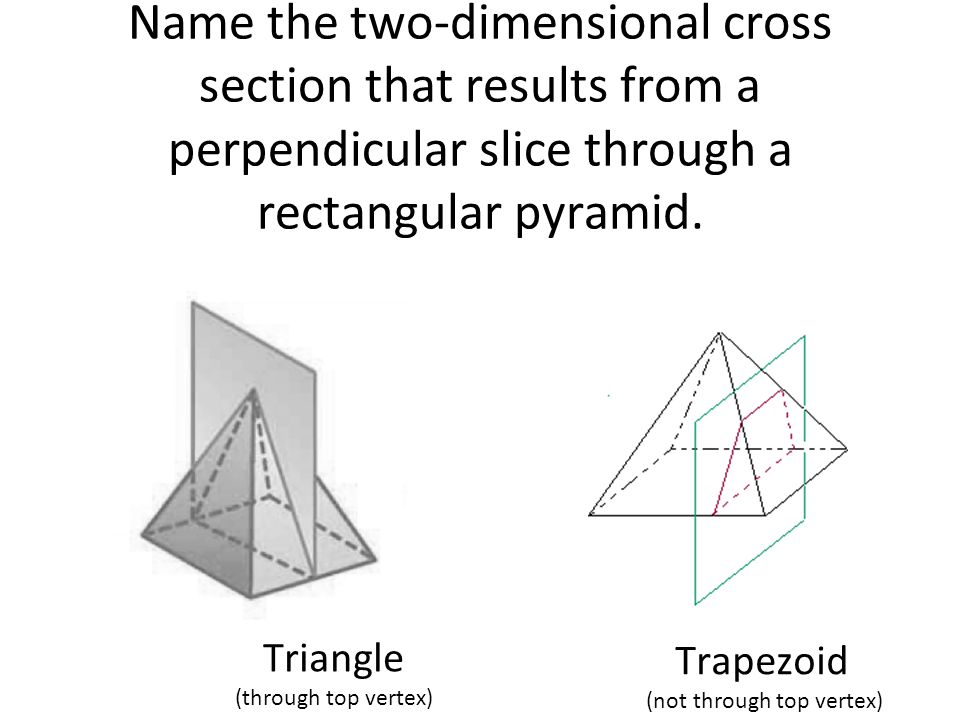
Do Now What Shape Would You Get If You Cut Through The Stick Of Butter Give The Most Specific Name Ppt Video Online Download

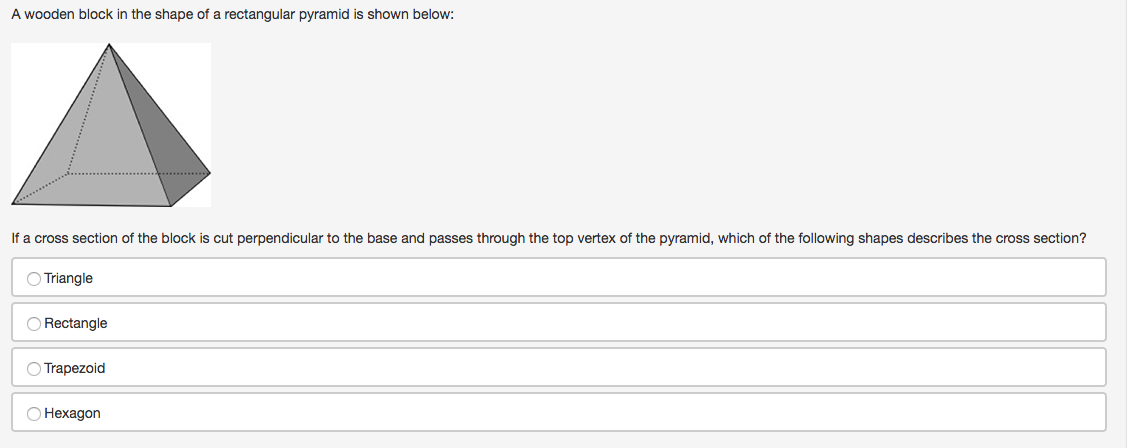
Answered A Wooden Block In The Shape Of A Bartleby

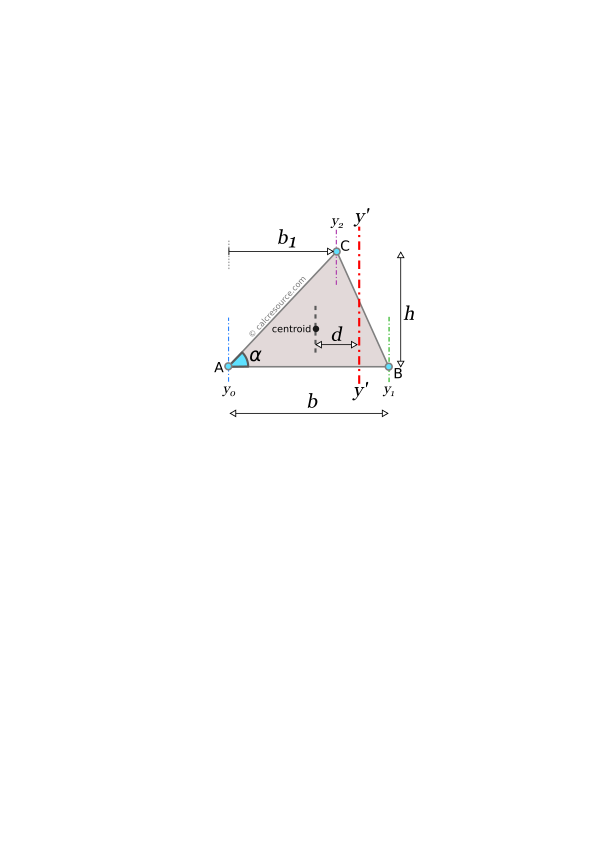
Moment Of Inertia Of A Triangle Calcresource

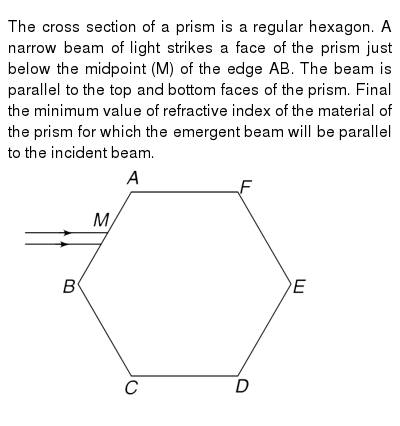
A Slice Is Made Perpendicular To The Base Of A Right Rectangular

D2y1pz2y Cloudfront Net 2904 Documents 19 2 11 1 Cross Sections And Solids Of Revolution Pdf

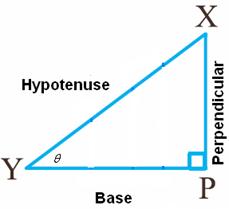
8 1 Trigonometric Ratios Sin Cos Tan

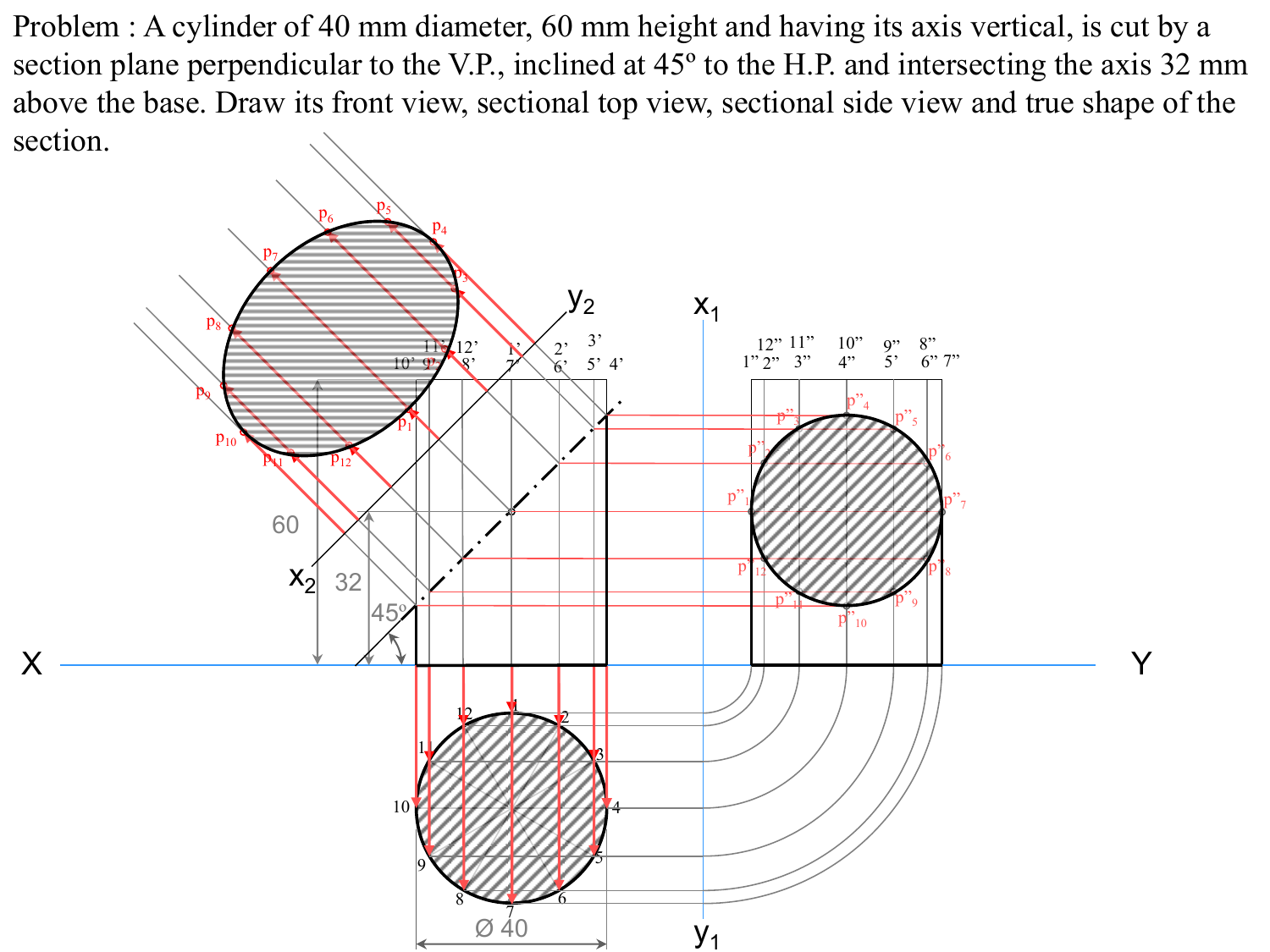
A Cylinder Of 40 Mm Diameter 60 Mm Height And Having Its Axis Manualzz

A Frustum With A Regular Pentagonal Base Is Such That Its Top Is Of Side 12cm And Bottom Is Of Side 24cm

Www Sps186 Org Downloads Basic 8 7b Pdf

Perpendicular Or Orthogonal Projection Of The Top Base Onto The Download Scientific Diagram

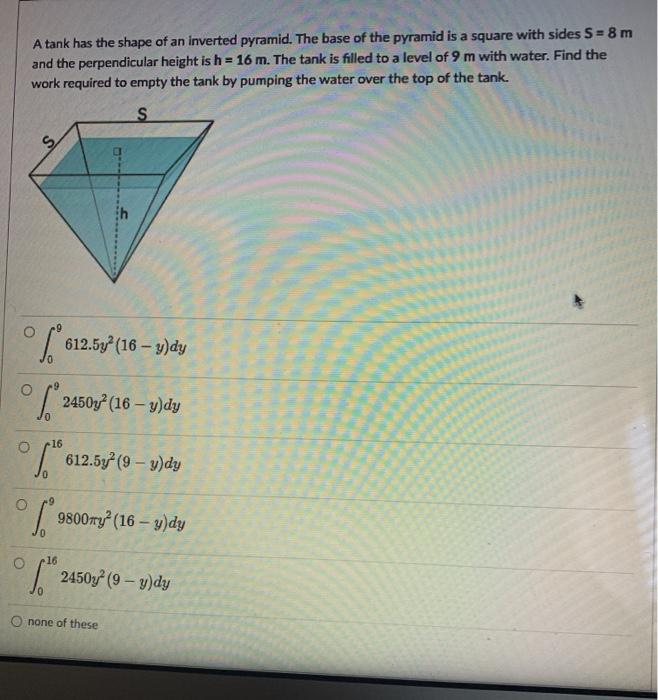
A Tank Has The Shape Of An Inverted Pyramid The Base Chegg Com

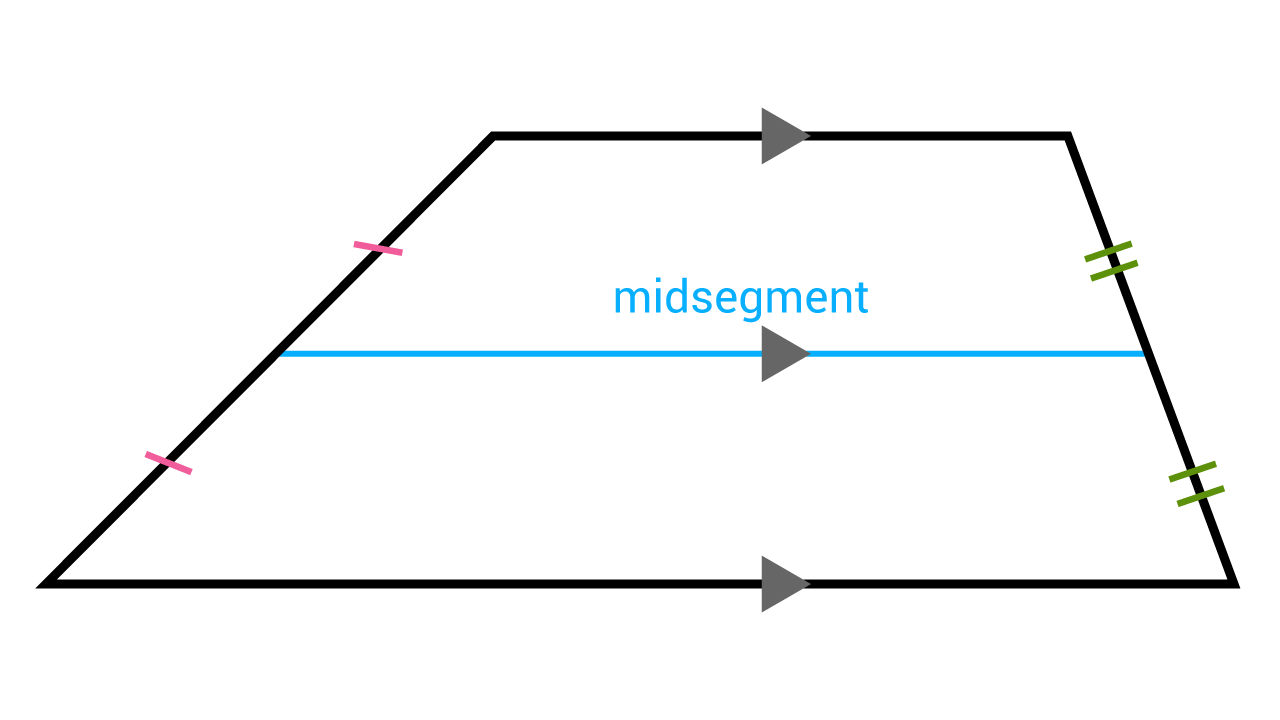
Trapezoid Properties Visually Explained W 7 Examples

Cross Sections Easy Peasy All In One Homeschool

Http Www Iitg Ac In Rkbc Me111 Lecture10 projection of solids Pdf

Chapter 1 Basic Terms And Calculations

Find The Volume Of A Pyramid Whose Base Is A Square With Side L And Whose Length Is H Sketch The Solid And Indicate How You Form The Integral Study Com

Volume Of A Solid With A Known Cross Section

2

6 2 Determining Volumes By Slicing Calculus Volume 1

The Dimensions Of A Square Right Pyramid Are Shown Below The Pyramid Is Sliced By A Plane That Brainly Com

13 2 Pyramids And Cones Three Dimensional Objects Siyavula

Cross Sections Parallel Cross Section Triangle Base Cross

How To Find The Area Of A Parallelogram Maths With Mum

Cross Sections Of Pyramids Ck 12 Foundation

Cross Sections Parallel Cross Section Triangle Base Cross

Trigonometry

Parallel Sides Parallel Shapes Tutors Com

How To Find The Point P Inside A Triangle Which Divides The Triangle When Connected With The Corners Into Three Triangles Of The Same Size Quora

Interactives 3d Shapes Glossary

Pyramid Calculator

Section Of Solid Pdf Perpendicular Triangle

Consider The Right Rectangular Pyramid And The Sli Gauthmath

Ssc Cgl 17 Tier2 Ratio Of Volume Of Regular Triangular Pyramid Cut By Planes Parallel To Base Youtube

Base And Height Of A Triangle Home Campus

Math Scene Triangles Lesson 1

Volume With Cross Sections Perpendicular To Y Axis Video Khan Academy

Perpendicular Wikipedia

1

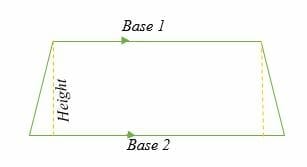
Area Of Trapezoid Explanation Examples

Example 8 Find The Volume Of A Pyramid Whose Base Is Chegg Com

Modern Welding 11th Edition Page 48 48 Of 6

Math Scene Triangles Lesson 1

Muthunathanespec Weebly Com Uploads 9 3 7 8 Unit Iv 2 Development Of Surfaces Pdf

Development Of Surface Square Pyramid Rajagopal Thangavel S Forum Youtube

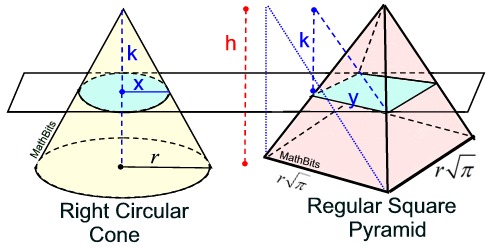
Cones Mathbitsnotebook Geo Ccss Math

A Top View Of The Gravel Bar With Two Perpendicular Gpr Profiles Download Scientific Diagram

Please Help Me I Cant What Is The Shape Of The Cross Section Of The Figure That Is Perpendicular To Brainly Com

Wl Apsva Us Wp Content Uploads Sites 38 17 02 7 2 Volume With Known Cross Sections Pdf

Two Plate Ab And Cd Are Rigidly Attached 1 Perpendic Physics

Calculus For Ap Sampler 531

Robotics Free Full Text Kinematics Of The 3 Rpsp S Fully Spherical Parallel Manipulator By Means Of Screw Theory

The Cross Section Of A Square Pyramid Taken Perpendicular To The Base That Passes Through The Top Vertex Produces Which Two Dimensional Shape Study Com

Theorem The Tangent At Any Point Of A Circle Is Perpendicular To The Radius Through The Point Of Contact Circles Class 10 Maths Geeksforgeeks

Study Island Pdf Rectangle Euclidean Plane Geometry

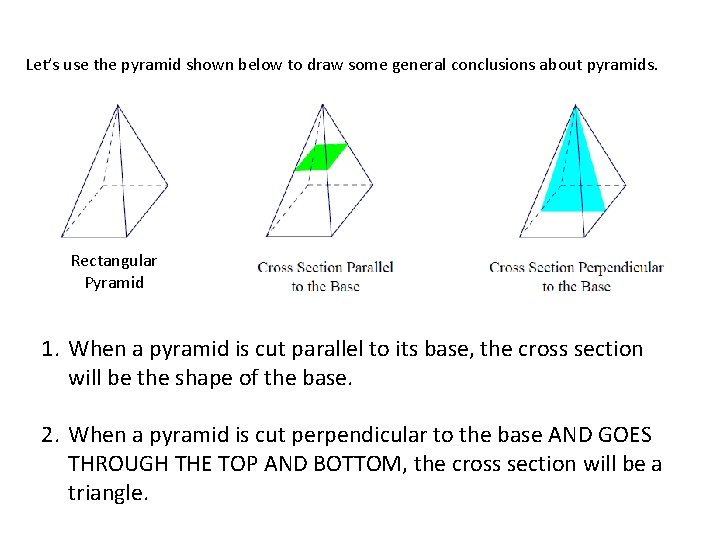
Cross Sections Parallel Cross Section Triangle Base Cross

Www Wrschool Net Cms Lib Az Centricity Domain 1627 Lesson 8 7 Pdf

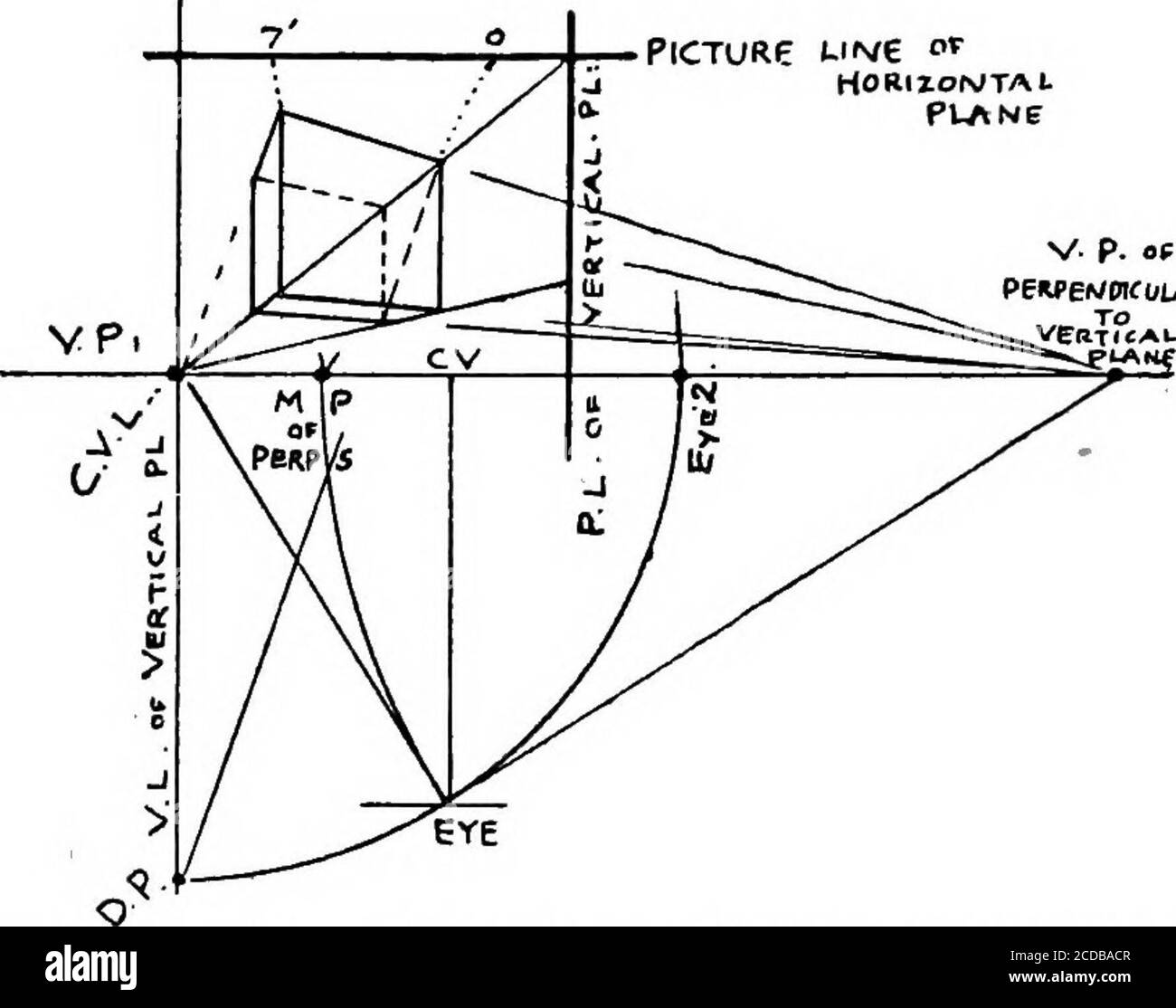
Perspective For Art Students Necessaryfor Obtaining A Perpendicular To An Oblique Plane Butare All The V L S And P L S Which Belong To A Rectangularobject With Base In An Oblique Plane Slanting

Square Pyramid Slices Students Are Asked To Sketch And Describe The Two Dimensional Figures That Res

Problem Suggested By User 0ceanaut Find The Volume Of Intersection Of Two Caps Within The Same Sphere With Perpendicular Base Planes Solution Only A Plan Without Final Calculations It S A Typical Problem On Double Integration But As In A Case Of The

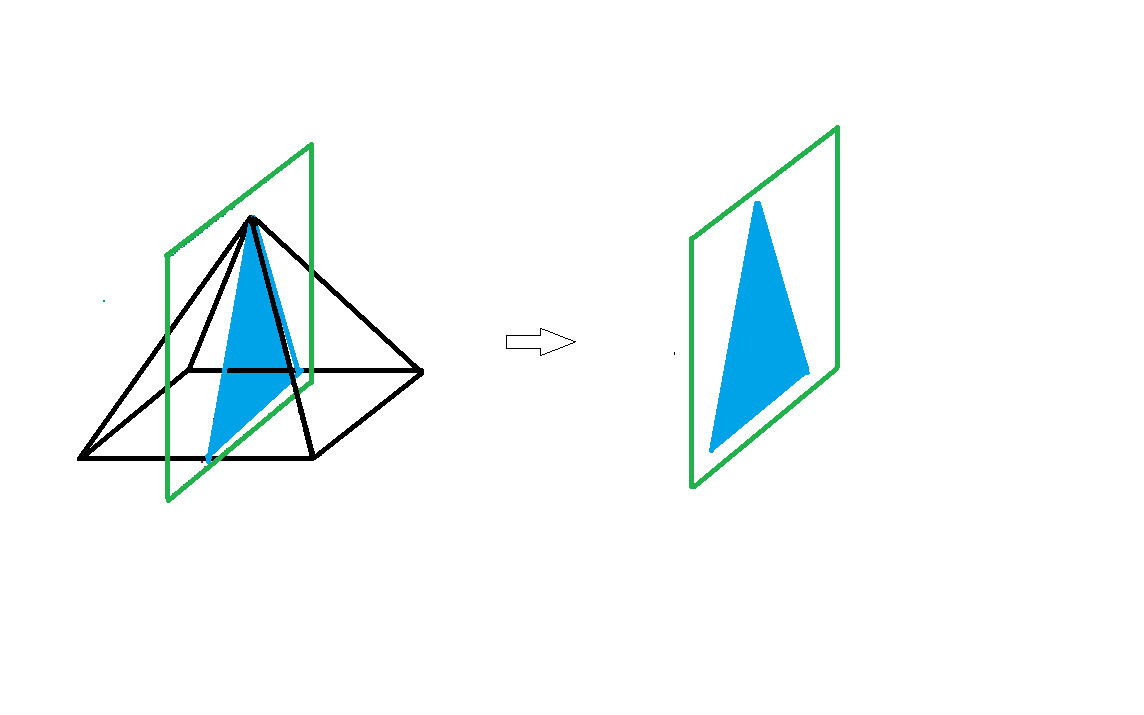
The Cross Section Of A Square Pyramid Taken Perpendicular To The Base That Passes Through The Top Vertex Produces Which Two Dime

Volume Of A Solid With A Known Cross Section

Two Plate Ab And Cd Are Rigidly Attached Perpendicul Physics

Www Math Tamu Edu Mvorobet Math152 S13 S7 2 S Pdf

Polyhedrons Regular Polyhedron Prism Pyramids Videos And Examples

Slicing 3 D Shapes Solutions Examples Videos Worksheets Activities

Section Development Engineering Graphics

3 Ways To Calculate The Volume Of A Square Pyramid Wikihow

A Square Pyramid Of Base Side 25mm And Altitude 50mm Rests On Its Base On The Hp With Two Sides Of The Base Parallel To Vp

Base Lateral And Surface Areas Of Prisms Ck 12 Foundation

Question 4 23 Marks A Vertical Cylinder Of Base Chegg Com

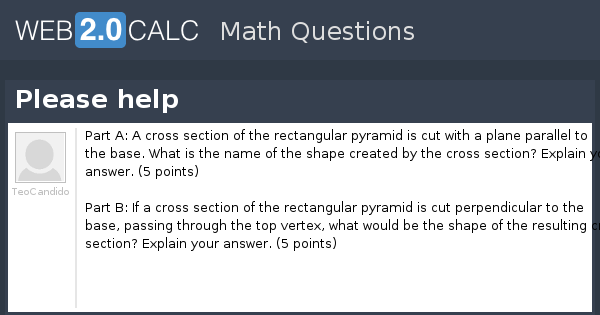
View Question Please Help

How To Find The Area Of A Trapezoid Formula Video Tutors Com